CS61B 学习笔记 - Quicksort

多年以后，在面对图灵奖时，Tony Hoare 仍会记得一个新手程序员尝试对单词列表进行排序的那个下午（）

另外，这节课的讲师换人了，是他的 secret ruler twin brother

Quicksort

快速排序的想法其实非常简单：选择，分区，然后递归

1. 选择一个元素作为 pivot，一般选择最左边第一个元素

2. 小于等于 pivot 的放在 pivot 的左边，大于 pivot 的放在 pivot 的右边，这样一来 pivot 的位置就确定了

3. 递归地对 pivot 的左边 Quicksort

4. 递归地对 pivot 的右边 Quicksort

快速排序的演示链接在这里

Tony Hoare 将其命名为 Quicksort，而且直到现在，在大多数情况下，快速排序仍然是最快的算法

快速排序的最佳运行时间是 Θ(NlogN)。分区用时 Θ(N)，有 Θ(logN) 层

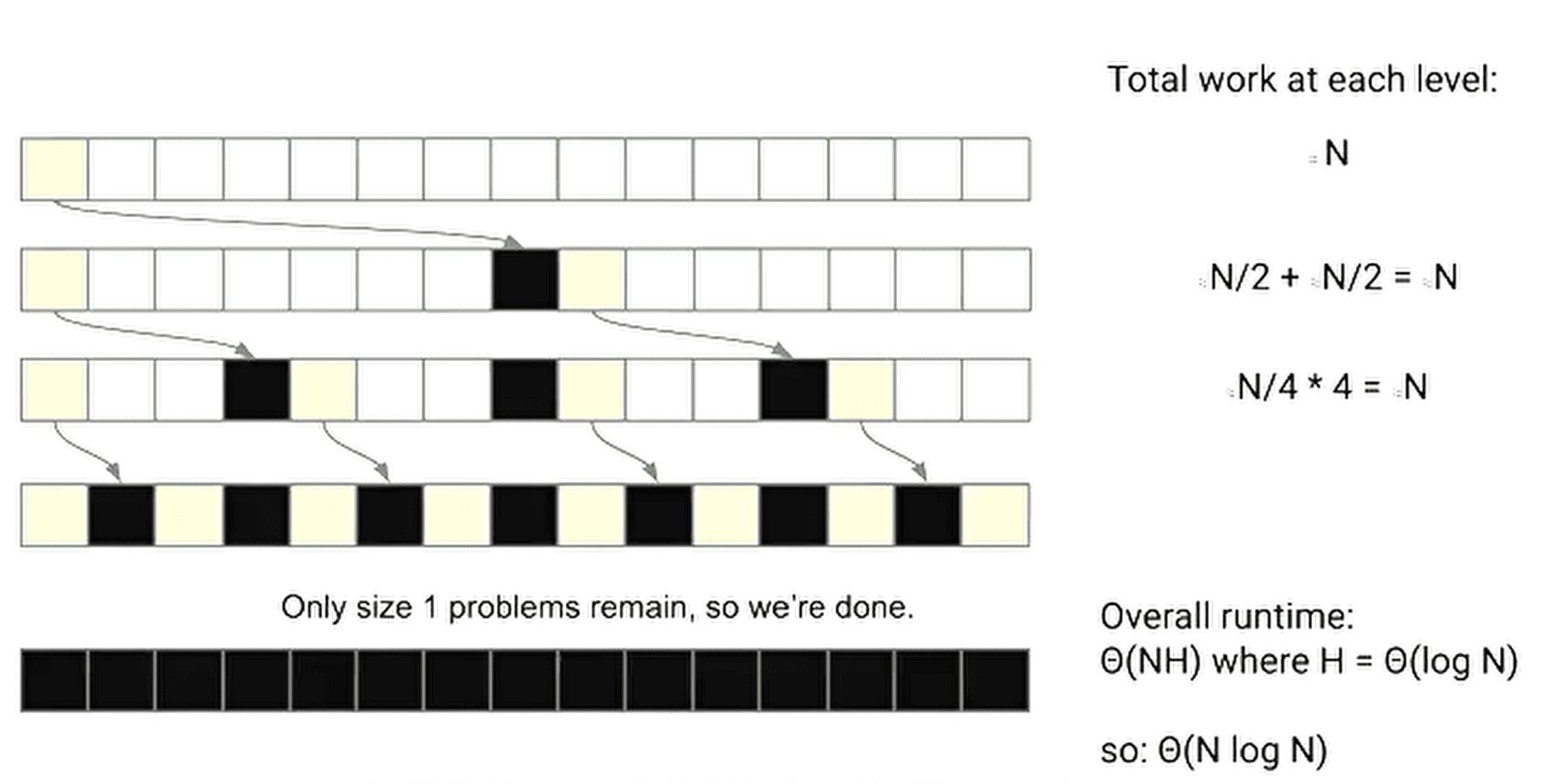
但是排序一个已经排好的数列，就会触发最坏运行时间 Θ(N²)

但是现实中除非故意为之，几乎不可能遇到这种情况：第一次选择 pivot 便是数组中的最大/最小值概论较小，但并非不可能，不过连续几十次几千次都是如此就几乎不可能出现了。因此，快速排序的时间复杂度往往是 Θ(NlogN)，且一般在 ~2N lnN 次比较后可以完成

下面这张图是对 N = 1000 的数组进行快速排序所需操作次数的分布情况。至于 Θ(N²)，10⁶ 都不在图上

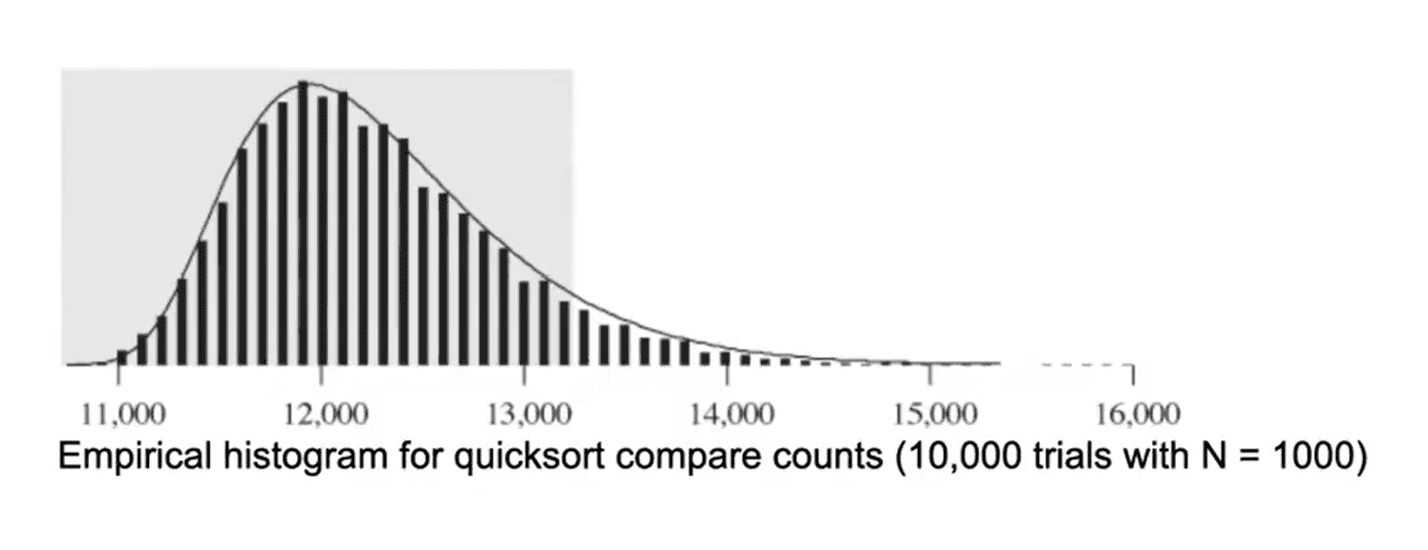
虽然快速排序与归并排序都是 O(NlogN)，但是快速排序往往比归并排序要快。（这可能是由于缓存，页命中等更加底层的东西决定的，没有细讲）

Quicksort Flavors

我们怎么做才能避免快速排序的最坏情况呢？那么就让我们来”定制化“一个快速排序吧，从 pivot 选择算法，Partition 算法，到 预处理算法，都有改进地空间。一下是一些改进的思路：

Philosophy 1: Randomness

最坏情况运行时的一些可能原因包括：

1. 数组已经排序

2. 数组有大量重复的元素（甚至全部一样）

对应的方法是：

1. 随机选择 pivot

2. 在排序之前提前打乱 items（Shuffle items before sort）

Philosophy 2: Smarter Pivot Selection

1. 我们可以先抽几个 items，然后从 items 中取一个最合适的作为 pivot（但是仍然防不住有人恶意攻击）

2. 有一种算法可以在 Θ(N) 时间找出中位数，这样就不会有上面的漏洞了。但虽然时间仍是 Θ(NlogN)，却比归并排序慢了

Philosophy 3: Introspection

我们可以设置这样一个机制：当察觉时间不对劲时，我们切换成归并排序

Although this is a reasonable approach, it is not common to use in practice.

Tony Hoare's Partioning

想想一下有两个指针，一个在数组的开头，一个在数组的末尾

在开头的指针，也就是左边的指针，喜欢比 pivot 更小的 item

在结尾的指针，也就是右边的指针，喜欢比 pivot 更大的 item

好，现在他们相对走去，如果遇到了不喜欢的 item，那就停下。如果两个指针都停下了，那就交换二者指向的元素，继续走

就这么一直重复，直到二者相遇

这里是关于这个算法的演示

我们可以看到，使用这种方法后有明显的优化

Quick Select

我们也可以利用这种想法快速查找中位数：

1. 初始化数组，将最左边的项目作为 pivot

   

2. 分区

   

3. 重复此过程

   9 处在中位之左，故 9 即其左边都舍弃不看

   

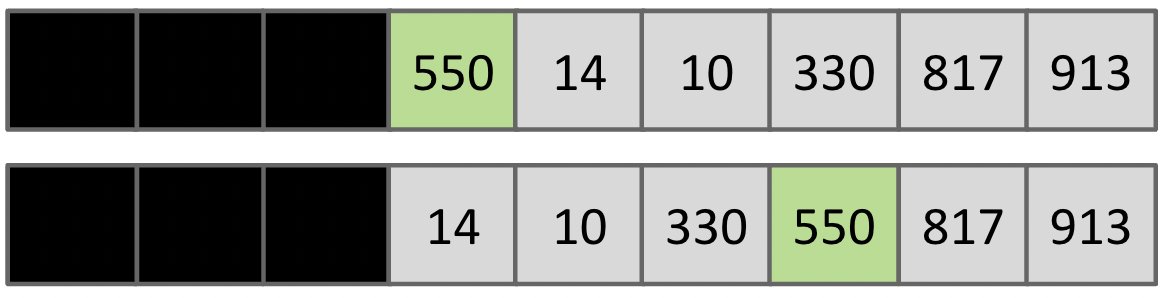
4. 直到 pivot 处于数组中间停止

   

运行时间：N + N / 2 + N / 4 + ...... + 1 = Θ(N)